Tuning the task allocator

By default, the objective of the allocator is to minimize the total energy consumption of the network. A few other predefined objective functions are also available (minimize the maximal energy consumption on a single node, maximize the remaining energy after a user-defined time period). However, the user can also write his own objective functions, specify them in the web interface, and use them for task allocation.

Similarly, the tool offers a few predefined constraint classes, but the user is allowed to write his own.

Also, the default task allocation strategy may take large time to find the optimal solution in large and medium-size networks. The user having full knowledge of his network and task graph may be able to specify a more efficient search strategy, so he’s allowed to do so.

Familiarity with Gecode or at least constraint programming in general is advised for this tutorial.

The task graph and network
A custom constraint
A custom objective function
A different constraint
A custom search strategy
Download

The task graph and network

In this tutorial, we will work with a simple sense-and-send application in an unconstrained mesh network. This is a fairly classical WSN setup.

Draw a number of sensing tasks and connect them to data collector:

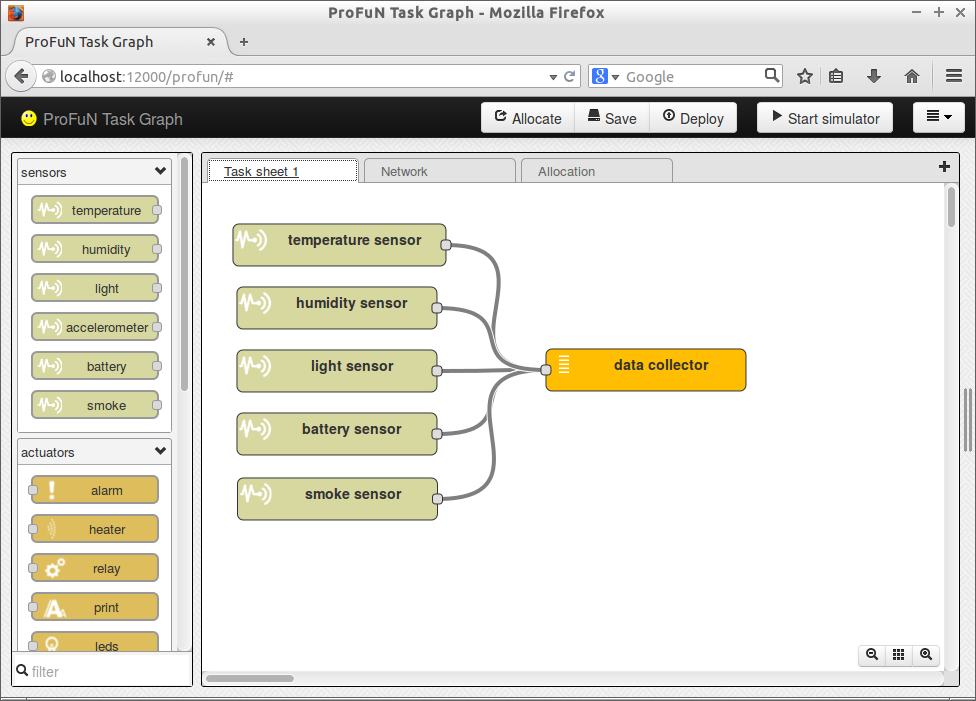
Create a mesh network of nodes all capable of hosting all sensors (edit the capabilities in template configuration dialog):

The allocation produced by default puts all tasks on a single node:

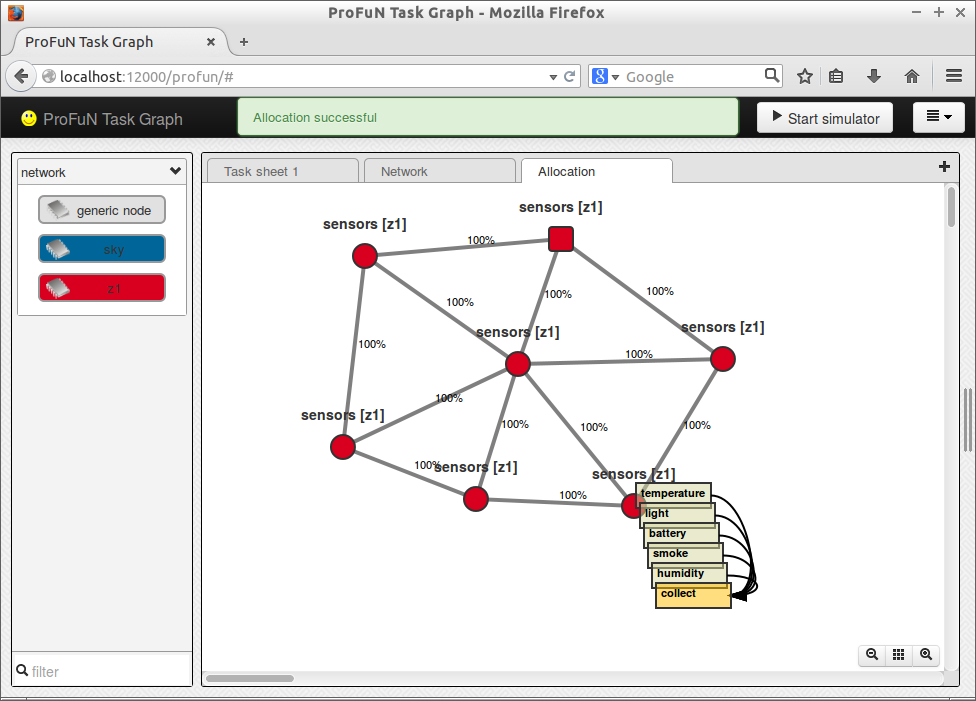
A custom constraint

There may be a number of reasons why the mapping produced above is unsatisfactory.

For example, each sensing task may take non-negligible amount of energy to perform. That energy is not accounted by the allocator by default - only energy for communication is modeled. Perhaps an unfair distribution of tasks may reduce the lifetime of the network even more than the extra energy spent for radio communications required to transmit data between nodes. Also, distributing the tasks between nodes may increase the reliability of the network, as well as its coverage in some sense. Finally, a large number of tasks on a single node may strain resources, for example, not fit into RAM.

Because of these reasons, let’s say that we want to have no more than two tasks on each node.

Open “Task allocation options” configuration dialog. Select “CUSTOM” objective function - the constraint is simply specified as part of the function!

The ideas is to reuse already existing objective function. The prototypes of objective functions can be found in file taskalloc/of.h:

double estimateNetEnergyExpectedValue(const Gecode::ViewArray<Gecode::Int::IntView> &, bool &finished);
double estimateNetMaxEnergyValue(const Gecode::ViewArray<Gecode::Int::IntView> &, bool &finished);
double estimateNetRemainingEnergyValue(const Gecode::ViewArray<Gecode::Int::IntView> &, bool &finished);

#if INCLUDE_CUSTOM_OBJECTIVE_FUNCTION
#warning Enabling a custom objective functions
double customObjectiveFunction(const Gecode::ViewArray<Gecode::Int::IntView> &);
#endi

The first three functions correspond to the first three options in the dialog (optimize for total energy, optimize for maximal energy, and optimize for remaining energy).

The block under #if INCLUDE_CUSTOM_OBJECTIVE_FUNCTION shows the signature of the custom function. The C++ code specified in the dialog is essentially is going to become the body of that function.

Let’s start writing it. The idea is to first check if the mapping does not violate the maximum number of tasks constraint. If it does, reject the mapping by returning infinitely large cost. If there is no violation, just return the value of the estimateNetEnergyExpectedValue function.

Here’s the code in full:

// find out the number of tasks allocated on each node
vector<unsigned> numOnNodes(numNodes());
for (auto& t : TaskAllocator::taskGraph->taskMap) {
  if (v[t->id].assigned())
    numOnNodes[v[t->id].val()]++;
}

for (const auto& n : numOnNodes) {
  // if the number of tasks is greater or equal to three
  if (n >= 3) {
    return INFINITY;
  }
}

// use a predefined function to find the energy cost
return estimateNetEnergyExpectedValue(v);

The line for (auto& t : TaskAllocator::taskGraph->taskMap) iterates for all tasks. The condition if (v[t->id].assigned()) checks if the mapping for that task has already been fixed. (Required, because the evaluation function may be called on incomplete mappings. That allows to increase the performance of the allocation algorithm, as some mapping can be rejected even before they are completed.)

The array numOnNodes accumulates the number of tasks mapped on each node. The second for loop simply checks for the condition of the constraint.

Now when you push the “Allocate” button, the process takes a bit longer. First, the Python daemon rebuilds the C++ application to include the custom objective function (C++ compiler and some third-party libraries are required for this step). Then, the allocator application is executed as usual. If this application crashes (for example, because of a faulty code in the custom objective function), the Python daemon simply logs this event, and responds to the client with an error message. The stability of the system is not compromised, at least as long as the errors are not malevolent. (Of course, writing and executing custom objective functions should be allowed only for trusted users!)

Tip: Don’t put potentially slow code in the objective function, for example, don’t use endl with iostreams!

The result of this objective function:

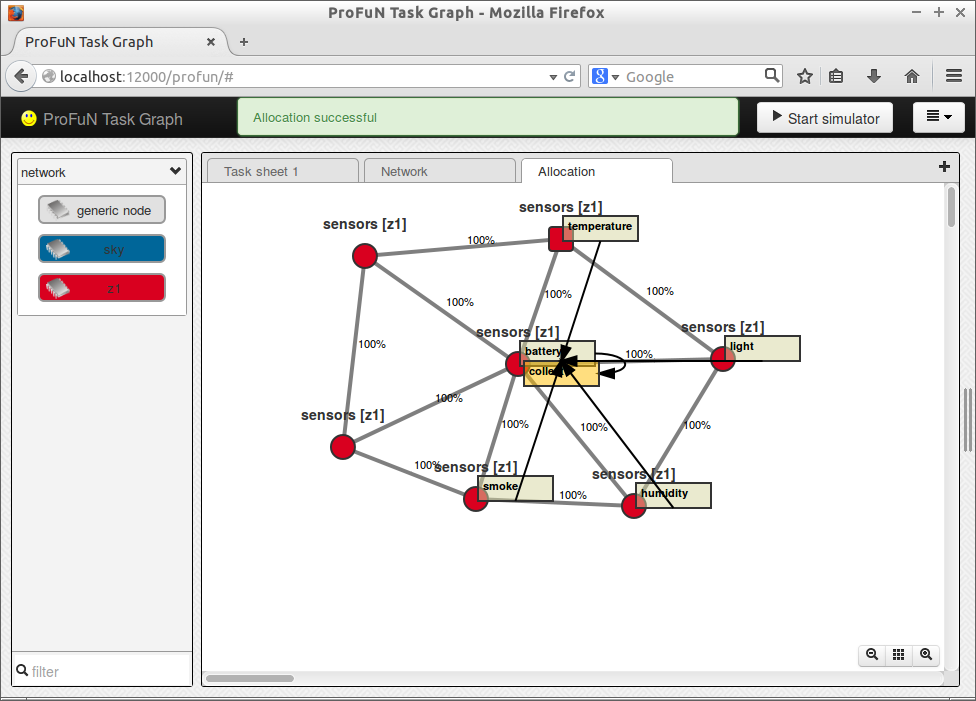
No nodes have more than two tasks.

Of course, the custom constraint can also be added by modifying the code of the task allocator itself. However, when specified through the frontend, the constraint is part of the model. This means:

To produce the same allocations on several different computers, just the model file must be shared, not modifications in C++ files.
Custom constraints and objective functions are model-specific; they do not change the default behavior of the allocator.

A custom objective function

In many cases, “bad” task mappings should not be rejected out of hand; they simply should be penalized.

This problem is a little more difficult, as now it’s not a binary decision problem anymore. The penalty should be a number (most likely, double), and deciding its magnitude may be nontrivial. Still, the approach here is the same: write a block of custom C++ code in the task allocation option dialog.

One idea how to decide the magnitude of the penalty is not to use a fixed number for each case of “badness” detected, but instead make the penalty proportional to the cost the mapping. Such a method is relatively robust against variations both in the the scale of the network and changes in the objective function.

Specifically here we’re going to use penalty with linear scale (n points of “badness” make the penalty n times larger) that is also linearly proportional to the energy cost of the mapping. Exponential and constant-amount penalty functions also often are useful.

The code is just a bit more complex:

double penalty = 1.0;

// find out the number of tasks allocated on each node
vector<unsigned> numOnNodes(numNodes());
for (auto& t : TaskAllocator::taskGraph->taskMap) {
  if (v[t->id].assigned())
    numOnNodes[v[t->id].val()]++;
}

for (const auto& n : numOnNodes) {
  // if the number of tasks is greater or equal to three
  if (n >= 3) {
    penalty += n - 2;
  }
}
// use a predefined function to find the energy cost
double netEnergyEV = estimateNetEnergyExpectedValue(v);
netEnergyEV += 1.0;
return netEnergyEV * penalty;

Here we start with calculating the expected energy consumption; then the constraint condition is evaluated and checked. Finally, a penalty is applied to the energy cost.

One tricky aspect is shown in the line netEnergyEV += 1.0;. Because the penalty function scales linearly with the energy costs, zero cost receives no penalty. This is the point where the robustness of this approach breaks down. In order to avoid such fixed points, the minimal energy is artificially changed to 1.0.

The mapping in this case is the same as shown above; however, the difference is that in a less resource-rich network it would not fail.

A different constraint

In some cases, it is convenient to have different tasks co-located. For example, we might want to have temperature and humidity sensing tasks on the same node. Humidity sensors usually produce relative humidity value, which is temperature dependent. As a result, measuring humidity often also involves internally measuring temperature, so humidity sensors are combined with temperature sensors. This means that sensing temperature only when humidity is already sensed allows to significantly reduce energy consumption, because just one instead of two distinct sensors are going to have to be switched on.

Let’s improve our model with the constraint that the two sensors must be on same node. Change the type of numOnNodes array: let it store an array of Task *, not integers:

vector<vector<Task *>> numOnNodes(numNodes());

Now, additional loop can be written to check the constraint:

for (const auto& tasks : numOnNodes) {
  // check for the custom constraint
  bool hasTemperature = false;
  bool hasHumidity = false;
  for (const auto& task : tasks) {
     if (task->name == "temperature")
       hasTemperature = true;
     else if (task->name == "humidity")
       hasHumidity = true;
  }
  // if not both or none, reject this mapping
  if (hasTemperature != hasHumidity) return INFINITY;
}

The loop simply checks task names. Be aware that if our model had a custom-named temperature or humidity task, the code would fail to identificate them as such!

Incorporate this code in the previous objective function. The result is:

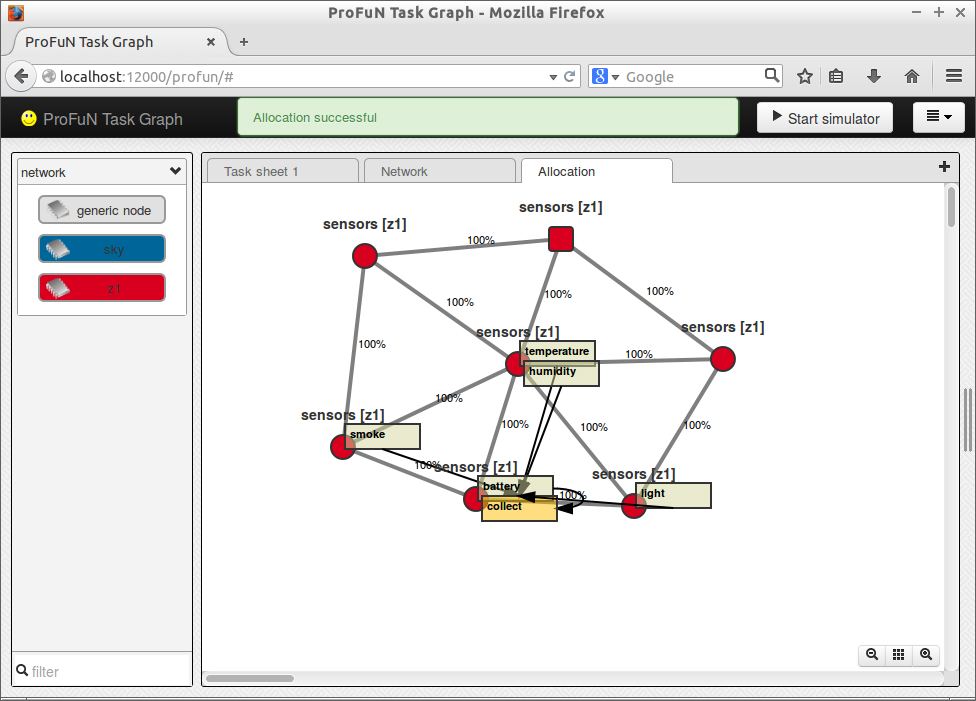
A custom search strategy

Gecode offers many options to control the order in which the solution space is searched. Changes in these options are not going to affect the resulting allocation (discounting different allocations with exactly the same cost), but they can have large impact of the allocation performance.

In particular, the task allocator software by default defines a custom task selection order in the branching process (by function int_merit), and a custom task-to-node assignment order (by function int_val_same).

The rationale of the first function is start the mapping with the tasks that are most likely to remain in their places once assigned: tasks that have the highest number of constraints and connections to other tasks. The rationale of the second is to map the second tasks in a communicating pair either on the same node as the first, or on nodes close (directly connected) to the nodes.

However, for some networks the functions, in particular int_val_same, has been shown to give significantly worse performance than some of the default options offered by Gecode. So the user is allowed to change them.

Let’s see the statistics for the network with default branching:

    runtime:      0.524 (524.511 ms)
    solutions:    673
    propagations: 206486
    nodes:        235297
    failures:     116976
    restarts:     0
    no-goods:     0
    peak depth:   15

Good results are also typically achieved by value selection function INT_VAL_RANGE_MAX(). Let’s try it. In the “Branching code” field of the options dialog, enter:

branch(*this, v, INT_VAR_MERIT_MAX(int_merit), INT_VAL_RANGE_MAX());

Results:

    runtime:      0.503 (503.332 ms)
    solutions:    673
    propagations: 150053
    nodes:        235297
    failures:     116976
    restarts:     0
    no-goods:     0
    peak depth:   18

Now also change the order selection function. INT_VAR_NONE() is a default offered by Gecode: as the next one select any task that has not been assigned any node yet.

branch(*this, v, INT_VAR_NONE(), INT_VAL_RANGE_MAX());

Results:

    runtime:      0.503 (503.931 ms)
    solutions:    673
    propagations: 118880
    nodes:        235297
    failures:     116976
    restarts:     0
    no-goods:     0
    peak depth:   18

Interestingly, the branching order in this case almost doesn’t change the statistics (except for the number of propagations and peak search depth), but actually produces a different allocation: one where every task share the same node. It turns out that the penalty specified earlier was just large enough to even out the extra communication costs required.

Download

The resulting model files are available:

ProFuN Task Graph documentation